06: Age structured populations

Fallert, S. and Cabral, J.S.

Many species have population dynamics that can’t be described by a simple Ricker model. A common abstraction to deal with this complexity is to partition a species into functional subgroups that undergo different processes, as for example juveniles who are dispersing and looking for a habitat, who then become adults who are stationary but have the ability to reproduce and generate the next generation of juveniles. The following illustrates how to model such a system.

Basic setup

library(metaRange)
#> metaRange version: 0.0.0.9000
library(terra)
#> terra 1.7.55

Setup the basic simulation.

sim <- create_simulation(create_example_landscape())
sim$add_species("species_1")

Traits

Now we add the traits for both the juveniles and adults.

sim$add_traits(
    species = "species_1",
    n_juveniles = 100,
    n_adults = 100,
    mortality_juveniles = 0.1,
    mortality_adults = 0.7,
    reproduction_rate = 2
)
sim$add_traits(
    species = "species_1",
    population_level = FALSE,
    dispersal_kernel = calculate_dispersal_kernel(
        max_dispersal_dist = 8,
        kfun = negative_exponential_function,
        mean_dispersal_dist = 4
    )
)

Processes

Now we add some processes that manage the transition between the age classes.

sim$add_process(
    species = "species_1",
    process_name = "reproduction",
    process_fun = function() {
        self$traits[["n_juveniles"]] <-
            self$traits[["n_adults"]] + (
                self$traits[["n_adults"]] * self$traits[["reproduction_rate"]]
            ) * self$sim$environment$current$habitat
    },
    execution_priority = 1
)
sim$add_process(
    species = "species_1",
    process_name = "getting_older",
    process_fun = function() {
        self$traits[["n_adults"]] <-
            self$traits[["n_adults"]] +
              self$traits[["n_juveniles"]] * (1 - self$traits[["mortality_juveniles"]])
    },
    execution_priority = 3
)

More processes

And some more for the dispersal and mortality.

sim$add_process(
    species = "species_1",
    process_name = "dispersal_of_juveniles",
    process_fun = function() {
        self$traits[["n_juveniles"]] <- dispersal(
            abundance = self$traits[["n_juveniles"]],
            dispersal_kernel = self$traits[["dispersal_kernel"]]
        )
    },
    execution_priority = 2
)
sim$add_process(
    species = "species_1",
    process_name = "mortality_of_adults",
    process_fun = function() {
        self$traits[["n_adults"]] <-
            self$traits[["n_adults"]] * (1 - self$traits[["mortality_adults"]])
    },
    execution_priority = 4
)

Result

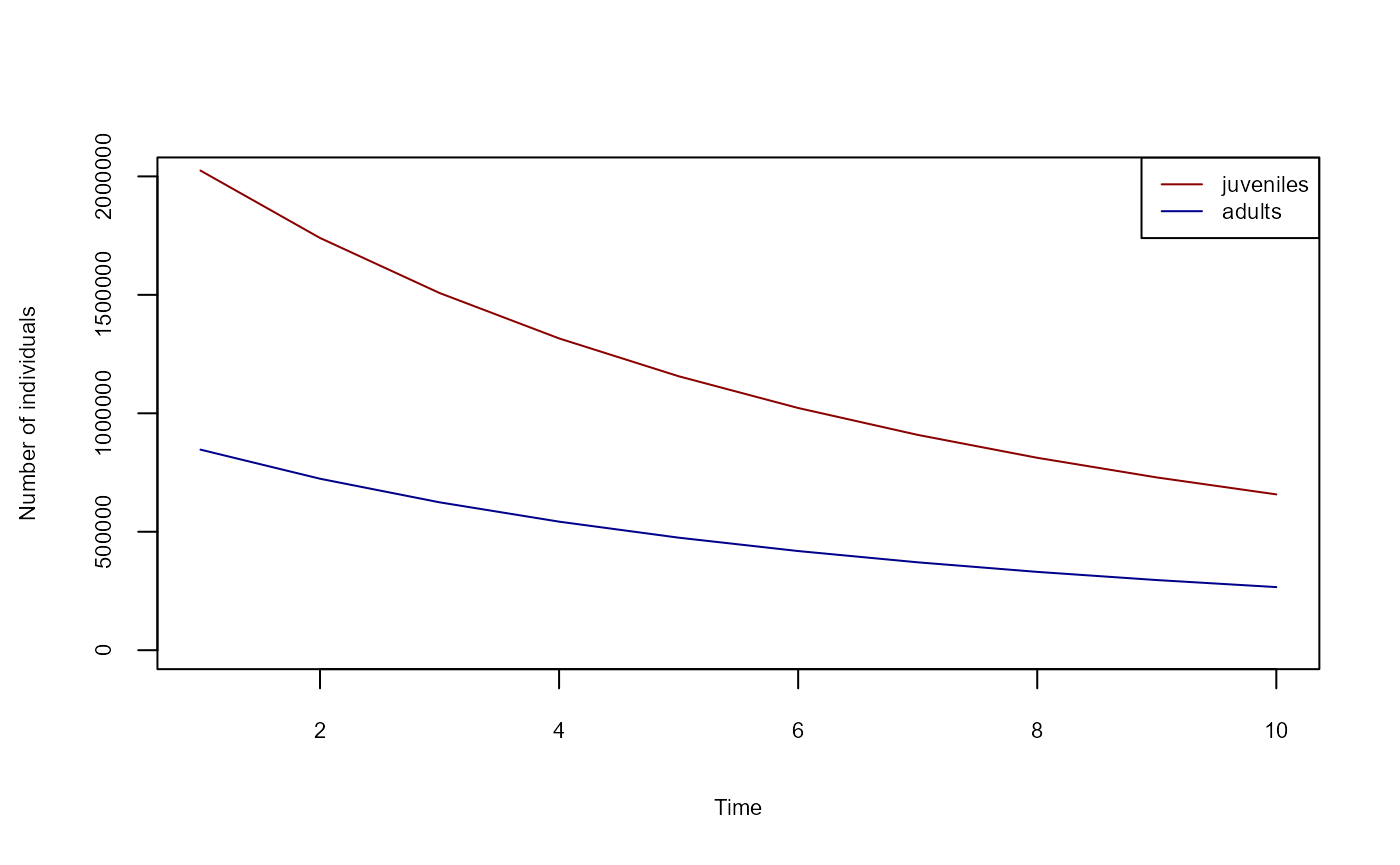
Lastly, we add a process that reports the numbers of adults and juveniles over time, then execute the simulation and plot the results.

sim$add_globals(n_juveniles = c(), n_adults = c())
sim$add_process(
    process_name = "logger",
    process_fun = function() {
        self$globals$n_juveniles <-
            c(self$globals$n_juveniles, sum(self$species_1$traits[["n_juveniles"]]))
        self$globals$n_adults <-
            c(self$globals$n_adults, sum(self$species_1$traits[["n_adults"]]))
    },
    execution_priority = 5
)
sim$begin()
plot(
    1:10,
    sim$globals$n_juveniles,
    col = "darkred",
    type = "l",
    ylim = c(0, 2000000),
    xlab = "Time",
    ylab = "Number of individuals",
    cex.lab = 0.7,
    cex.axis = 0.7
)
lines(1:10, sim$globals$n_adults, col = "darkblue")
legend(
    "topright",
    legend = c("juveniles", "adults"),
    col = c("darkred", "darkblue"),
    lty = 1,
    cex = 0.7
)